Cutting Length of Triangular Stirrups

The cutting length of the triangular stirrup is done by using Simple and easy formula.

Let’s solve this example for your better understanding.

EXAMPLE:

Suppose we are using a triangular stirrup in a column and a column having a Length 500 mm and having a Width 500 mm (X-section). The clear cover in the column will be 40 mm and the stirrup bar is going to use is 10 mm.

1. Calculate the cutting length of the triangular stirrup?
2. Also, calculate its weight?

GIVEN DATA:

Length of column = 500mm.

Width of column = 500 mm.

Clear cover = 40 mm.

Stirrup bar diameter = 10 mm.

length of the stirrup =?

The weight of the stirrup =?

SOLUTION:

The calculation of the triangular stirrup is to be done in 2 steps. In the first step, we calculate the Hypotenuse length of the right angle by using Pythagoras theorem. In the second step, we put these values into our given problem.

First A is the horizontal x section area and B is vertical x sectional area.

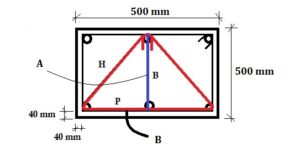
First we find A:

= 500 – (2 x clear cover) – (2 x half of dia of bar)

= 500 – (2 x 40) – (2 x 5)

= 500 – 80 – 10

= 410mm

Second  find B

= (500 – (2 x clear cover) – (2 x half of dia of bar))/2

= (500 – (2 x 40) – (2 x 5))/2

= (500 – 80 – 10)/2

= (410mm)/2

= 205 mm Ans…

Then we find the hypotenuse of the triangle

H=√(base)²+(Perpendicular)²

H=√A²+B²

H=√410²+205²

H = 458.39 mm

Cutting Length:

= (2 x H) + 2B + hook – bend

= (2 x H) + 2B + (2 x 10d) – (we have got 4 bends of 135 deg so minus 3d)

(Where d is dia of used in stirrups)

= (2 x H) + 2B + (2 x 10d) – (4 x 3d)

= (2 x 458.39) + 410 + (2 x 10 x 10) – (4 x 3 x 10)

= 916.78 + 410 + 200 – 120

= 1406.7mm or 1.406m

Weight of this stirrup:

= d²/162 x length

= 10²/162 x 1.406

= 0.867kg Ans…

Civil Notes App:-

1: Quantity surveying,

2: Concrete, 

3: Steel, Notes available in this Android App.

Click on the Below Picture to Download free from play store.

Civil Notes:- https://play.google.com/store/apps/details?id=com.engineering.civil.notes.clicks